MATRIZ INVERSA POR LA ADJUNTA

MATRIZ INVERSA POR LA ADJUNTA

En esta clase aprendimos lo que es una matriz adjunta para sacar la inversa de una matriz, con este metodo hacemos multiplicaciones cruzadas de la matriz restante de la posicion que queremos obtener la adjunta y asi con cada uno de estas posiciones, despues sacamos la transpuesta y luego la determinante de la matriz original y dividimos por cada uno de los numeros de la matriz adjunta ya transpuesta. 

Sea A una matriz cuadrada y regular de dimensión n, entonces la matriz inversa de A, A−1

, viene dada por

 

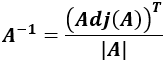
donde

• |A|

es el determinante de A  es la matriz adjunta o de adjuntos de la matriz A 

• signidica trasposición (matriz traspuesta), que se calcula cambiando filas por columnas. 

Nota: algunos autores llaman matriz adjunta a la traspuesta de la matriz adjunta que definimos a continuación.

Matriz adjunta:

Sea A

una matriz de dimensión mxn, denotamos al elemento de la fila i y columna j de A por ai,j

. Entonces, 

Con esta notación, si la matriz A

es de dimensión 2x2, tiene la forma

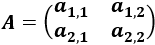
Y si es de dimensión 3x3,

La matriz adjunta de A

, Adj(A), tiene la misma dimensión que A y si denotamos por adi,j al elemento de la fila i y columna j de Adj(A)

, entonces

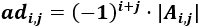
donde Ai,j

es la matriz que se obtiene al eliminar la fila i y columna j de A

(es una submatriz).

 

Ejemplo de submatriz

Consideremos la siguiente matriz A

de dimensión 3:

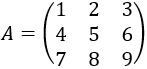
• La submatriz A2,2

se obtiene al eliminar la fila 2 y la columna 2 de A

• :

• 
  

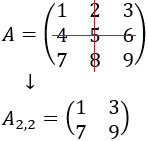
se obtiene al eliminar la fila 2 y la columna 3 de A

• 
  

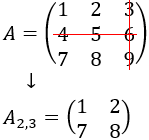
                                    La submatriz A2,3, se obtiene al eliminar la fila 2 y la columna 3 de A

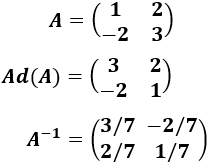
Fuente: https://www.matesfacil.com/matrices/resueltos-matrices-inversa-adjunta.html

Referencia del video: https://www.youtube.com/watch?v=NDepYHNe8fA